(本小题满分12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, 的部分图像如下图所示:
的部分图像如下图所示:
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)写出函数f(x)的递增区间.
(本小题满分12分)
已知|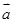 |=1,|
|=1,| |=
|= ;(I)若
;(I)若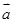 .
. =
=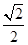 ,求
,求 与
与 的夹角;(II)若
的夹角;(II)若 与
与 的夹角为
的夹角为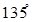 ,求|
,求|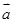 +
+ |.
|.
(本小题满分14分)已知函数 ,其中
,其中 .(1) 讨论函数
.(1) 讨论函数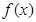 的单调性,并求出
的单调性,并求出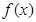 的极值;(2) 若对于任意
的极值;(2) 若对于任意 ,都存在
,都存在 ,使得
,使得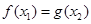 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知函数 (其中
(其中 且
且 为常数)的图像经过点A
为常数)的图像经过点A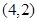 、B
、B .
. 是函数
是函数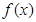 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点.
(1) 求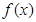 的解析式;
的解析式;
(2) 设 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列 满足
满足 ,记
,记 的前
的前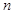 项和为
项和为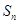 ,证明:
,证明: 。
。
(本小题满分12分)南昌市在加大城市化进程中,环境污染问题也日益突出。据环保局测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比.现已知相距18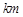 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为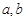 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设 (
(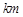 ).
).
(1) 试将 表示为
表示为 的函数;
的函数;
(2) 若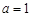 ,且
,且 时,
时, 取得最小值,试求
取得最小值,试求 的值.
的值.
(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.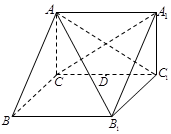
(1) 求证:平面AB1C1⊥平面AC1;
(2) 若AB1⊥A1C,求线段AC与AA1长度之比;
(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.