(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.
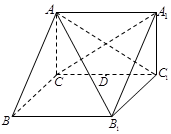
(1) 求证:平面AB1C1⊥平面AC1;
(2) 若AB1⊥A1C,求线段AC与AA1长度之比;
(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.
已知函数 的定义域为
的定义域为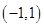 ,且同时满足下列条件:
,且同时满足下列条件:
(1) 是奇函数;
是奇函数;
(2) 在定义域上单调递减;
在定义域上单调递减;
(3) 求
求 的取值范围。
的取值范围。
已知集合A={x|x2-3x-10≤0},B={x|m+1≤x≤2m-1},若A∪B=A,求出实数m的取值范围。
已知p:方程x2+mx+1=0有两个不相等的负根;q:方程4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.
设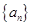 是公差不为零的等差数列,
是公差不为零的等差数列, 为其前
为其前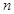 项和,满足
项和,满足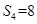 且
且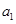 、
、 、
、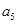 成等比数列.
成等比数列.
(Ⅰ)求数列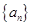 的通项公式;
的通项公式;
(Ⅱ)设数列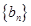 满足:
满足: ,
, ,
,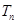 为数列
为数列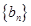 的前
的前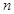 项和,问是否存在正整数
项和,问是否存在正整数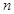 ,使得
,使得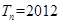 成立?若存在,求出
成立?若存在,求出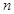 ;若不存在,请说明理由.
;若不存在,请说明理由.
设椭圆 的左、右焦点分别为
的左、右焦点分别为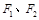 ,上顶点为
,上顶点为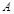 ,离心率为
,离心率为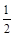 ,在
,在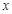 轴负半轴上有一点
轴负半轴上有一点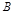 ,且
,且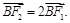
(Ⅰ)若过 三点的圆恰好与直线
三点的圆恰好与直线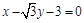 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(Ⅱ)在(Ⅰ)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆C交于
与椭圆C交于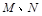 两点,在
两点,在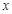 轴上是否存在点
轴上是否存在点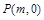 ,使得以
,使得以 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出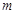 的取值范围;否则,请说明理由.
的取值范围;否则,请说明理由.