某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
(Ⅰ)从这20名学生中随机选出3名学生发言,求这3名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这20名学生中随机选出3名学生发言,设来自医学院的学生数为ξ,求随机变量ξ的概率分布列和数学期望.
已知函数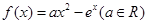
(Ⅰ)当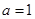 时,判断函数
时,判断函数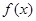 的单调区间并给予证明;
的单调区间并给予证明;
(Ⅱ)若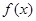 有两个极值点
有两个极值点 ,证明:
,证明: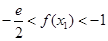 .
.
已知抛物线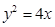 ,直线
,直线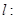
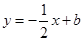 与抛物线交于
与抛物线交于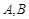 两点.
两点.
(Ⅰ)若 轴与以
轴与以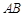 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(Ⅱ)若直线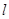 与
与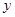 轴负半轴相交,求
轴负半轴相交,求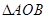 面积的最大值.
面积的最大值.
已知四棱锥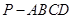 中,
中,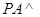 平面
平面 ,底面
,底面 是边长为
是边长为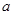 的菱形,
的菱形, ,
, .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)设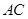 与
与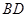 交于点
交于点 ,
,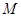 为
为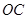 中点,若二面角
中点,若二面角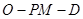 的正切值为
的正切值为 ,求
,求 的值.
的值.
市一中随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是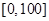 ,样本数据分组为
,样本数据分组为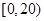 ,
,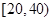 ,
,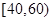 ,
,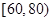 ,
,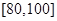 .
.
(Ⅰ)求直方图中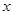 的值;
的值;
(Ⅱ)如果上学路上所需时间不少于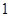 小时的学生可申请在学校住宿,若招生
小时的学生可申请在学校住宿,若招生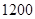 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的高一学生中任选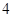 名学生,这
名学生,这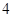 名学生中上学路上所需时间少于
名学生中上学路上所需时间少于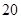 分钟的人数记为
分钟的人数记为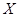 ,求
,求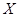 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
已知数列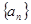 的各项均为正数,前
的各项均为正数,前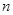 项和为
项和为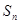 ,且
,且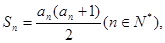
(Ⅰ)求证数列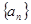 是等差数列;
是等差数列;
(Ⅱ)设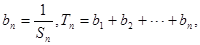 求
求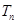 .
.