(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表,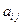 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为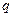 ,若已知
,若已知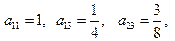
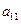 |
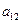 |
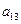 |
… |
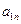 |
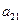 |
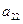 |
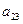 |
… |
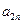 |
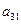 |
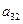 |
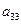 |
… |
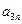 |
| … |
… |
… |
… |
… |
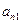 |
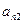 |
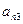 |
… |
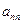 |
(1)求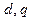 的值;
的值;
(2)求用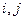 表示
表示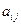 的代数式;
的代数式;
(3)设表中对角线上的数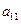 ,
,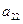 ,
,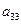 ,……,
,……,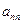 组成一列数列,设Tn=
组成一列数列,设Tn=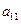 +
+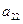 +
+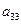 +……+
+……+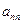 求使不等式
求使不等式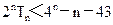 成立的最小正整数n.
成立的最小正整数n.
如图,在边长为1的正六边形ABCDEF中,其中心为点O.
(1)在正六边形ABCDEF的边上任取一点P,求满足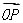 在
在 上的投影大于
上的投影大于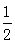 的概率;
的概率;
(2)从A,B,C,D,E,F这六个点中随机选取两个点,记这两个点之间的距离为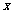 ,求
,求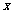 大于等于
大于等于 的概率.
的概率.
已知向量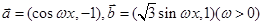 ,函数
,函数 图像的一条对称轴与其最近的一个对称中心的距离为
图像的一条对称轴与其最近的一个对称中心的距离为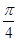 .
.
(1)求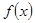 的解析式;
的解析式;
(2)在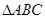 中,
中,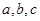 分别是角A,B,C的对边,
分别是角A,B,C的对边,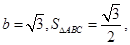
且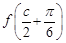
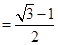 ,求边
,求边 的值.
的值.
(本小题满分10分)选修4—5,不等式选讲
已知函数
(1) 解关于 的不等式
的不等式 
(2)若不等式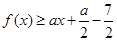 恒成立,求实数
恒成立,求实数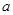 的取值范围;
的取值范围;
(本小题满分10分)选修4—4:坐标系与参数方程
在平面直角坐标系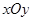 中,直线
中,直线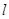 的参数方程为
的参数方程为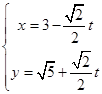 (
(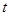 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系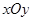 取相同的单位长度,且以原点
取相同的单位长度,且以原点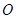 为极点,以
为极点,以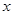 轴正半轴 为极轴)中,圆
轴正半轴 为极轴)中,圆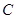 的方程为
的方程为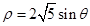 .
.
(1)求圆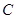 的直角坐标方程;
的直角坐标方程;
(2)设圆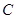 与直线
与直线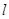 交于
交于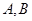 两点,若点
两点,若点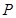 坐标为
坐标为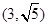 ,求
,求 .
.
(本小题满分12分)设函数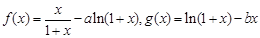 .
.
(1)若函数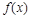 在
在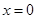 处有极值,求函数
处有极值,求函数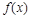 的最大值;
的最大值;
(2)①是否存在实数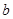 ,使得关于
,使得关于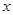 的不等式
的不等式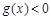 在
在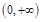 上恒成立?若存在,
上恒成立?若存在,
求出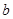 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式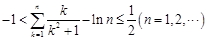 .
.