(本小题满分12分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动.若厂家投放A、B型号电视机的价值分别为p、q万元,农民购买电视机获得相应的补贴分别为 已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据:
已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据: ).
).
(1)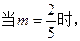 请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
(2)讨论农民得到的补贴随厂家投放B型号电视机金额的变化而变化的情况.
从4名男生和5名女 生中任选5人参加数学课外小组,求在下列条件下各有多少种不同的选法?
生中任选5人参加数学课外小组,求在下列条件下各有多少种不同的选法?
(1) 选2名男生和3名女生,且女生甲必须入选;
选2名男生和3名女生,且女生甲必须入选;
(2)至多选4名女生,且男生甲和女生乙不同时入选.
.(满分10分)由经验得知,在某商场付款处排队等候付款的人数及概率如下表:
| 排队人数 |
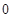 |
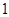 |
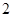 |
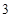 |
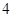 |
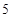 人以上 人以上 |
| 概率 |
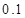 |
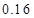 |
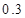 |
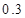 |
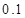 |
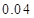 |
(I)至多有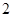 人排队的概率是多少?
人排队的概率是多少?
(II)至少有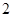 人排队的概率是多少
人排队的概率是多少
有一个容 量为100的样本,数据的分组及各组的频数如下:
量为100的样本,数据的分组及各组的频数如下:

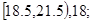
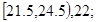
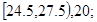

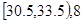
(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)估计数据小于30.5的概率。
.求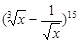 的展开式中的常数项和有理项.
的展开式中的常数项和有理项.
(本小题满分12分)
已知椭圆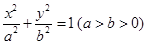 的长轴长为
的长轴长为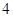 ,且点
,且点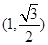 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点的直线 交椭圆于
交椭圆于 两点,若以
两点,若以 为直径的圆过原点,
为直径的圆过原点,
求直线 方程.
方程.