(本小题满分13分)设数列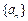 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:
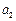
 ……
…… 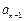
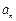 第1行
第1行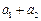
 ……
…… 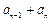 第2行
第2行
… … …
… …
… 第 行
行
上表共有 行,其中第1行的
行,其中第1行的 个数为
个数为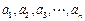 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若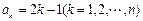 ,求和
,求和 .
.
如题18图,已知四棱锥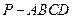 的底面是边长为2的正方形,
的底面是边长为2的正方形,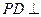 面
面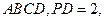
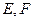 分别为
分别为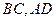 的中点.
的中点.
(Ⅰ)求直线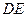 与面
与面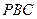 所
所 成的角;
成的角;
(Ⅱ)求二面角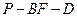 的大小.
的大小.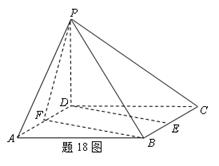
在一次数学考试中,共有10道选择题,每题均有四个选项,其中有且只有一个选项是正确的,评分标准规定:“每道题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有6道题是正确的,其余题目中:有两道题可判断两个选项是错误的,有一 道可判断一个选项是错误的,还有一道因不理解题意只好乱猜,请求出该考生:
道可判断一个选项是错误的,还有一道因不理解题意只好乱猜,请求出该考生:
(Ⅰ)得50分的概率;
(Ⅱ)设该考生所得分数为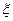 ,求
,求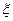 的数学期望.
的数学期望.
关于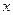 的不等式
的不等式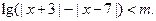
(Ⅰ) 当 时,解不等式;
时,解不等式;
(Ⅱ)设 函数
函数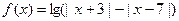 ,当
,当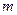 为何值时,
为何值时,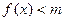 恒成立?
恒成立?
(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系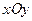 内,点
内,点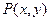 在曲线C:
在曲线C: 为参数,
为参数,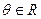 )上运动.以
)上运动.以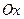 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线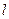 的极坐标方程为
的极坐标方程为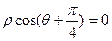 .
.
(Ⅰ) 写出曲线C的标准方程和直线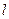 的直角坐标方程;
的直角坐标方程;
(Ⅱ) 若直线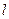 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求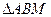 面积的
面积的
最大值.
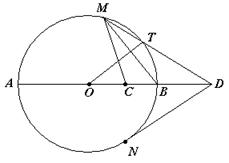
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1) 求证: ;
;
(2) 若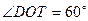 ,试求
,试求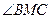 的大小.
的大小.