选修4－5：不等式证明选讲已知函数
．
（Ⅰ）试求
的值域；(Ⅱ)设
，若对
， 
，恒
成立，试
求实数
的取值范围
下面（a）（b）（c）（d）为四个平面图：
（1）数出每个平面图的顶点数、边数、区域数（不包括图形外面的无限区域），并将相应结果填入表：
| 顶点数 |
边数 |
区域数 |
|
| （a） |
4 |
6 |
3 |
| （b） |
12 |
||
| （c） |
6 |
||
| （d） |
15 |
（2）观察表，若记一个平面图的顶点数、边数、区域数分别为E、F、G，试推断E、F、G之间的等量关系；
（3）现已知某个平面图有2009个顶点，且围成2009个区域，试根据以上关系确定该平面图的边数．
试比较nn+1与（n+1）n（n∈N*）的大小．
当n=1时，有nn+1（n+1）n（填＞、=或＜）；
当n=2时，有nn+1（n+1）n（填＞、=或＜）；
当n=3时，有nn+1（n+1）n（填＞、=或＜）；
当n=4时，有nn+1（n+1）n（填＞、=或＜）；
猜想一个一般性的结论，并加以证明．
已知数列{an}的各项都是正数，且满足：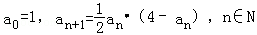
．
（1）求a1，a2；
（2）证明an＜an+1＜2，n∈N．
用数学归纳法证明不等式：
+
+
+…+
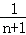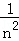＞1（n∈N*且n＞1）．
证明不等式
（n∈N*）