已知二次函数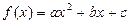 .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)若 对 ,方程
,方程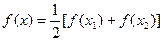 有2个不等实根,
有2个不等实根,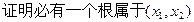 ;
;
(3)在(1)的条件下,是否存在m∈R,使f(m)=-a成立时,f(m+3)为正数,若
存在,证明你的结论,若不存在,说明理由.
(选修4-2:矩阵与变换)已知矩阵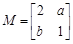 ,其中
,其中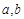 均为实数,若点
均为实数,若点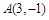 在矩阵
在矩阵 的变换作用下得到点
的变换作用下得到点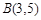 ,求矩阵
,求矩阵 的特征值.
的特征值.
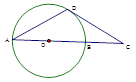
(选修4-1:几何证明选讲)如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若AB =" 2" BC ,
求证: .
.
(本小题满分16分)若数列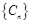 满足①
满足①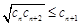 ,②存在常数
,②存在常数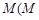 与
与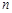 无关),使
无关),使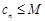 .则称数列
.则称数列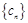 是“和谐数列”.
是“和谐数列”.
(1)设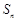 为等比数列
为等比数列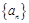 的前
的前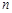 项和,且
项和,且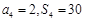 ,求证:数列
,求证:数列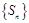 是“和谐数列”;
是“和谐数列”;
(2)设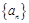 是各项为正数,公比为q的等比数列,
是各项为正数,公比为q的等比数列,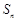 是
是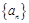 的前
的前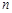 项和,求证:数列
项和,求证:数列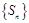 是“和谐数列”的充要条件为
是“和谐数列”的充要条件为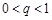 .
.
(本小题满分16分)已知函数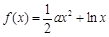 ,
,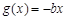 ,设
,设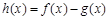 .
.
(1)若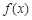 在
在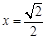 处取得极值,且
处取得极值,且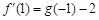 ,求函数h(x)的单调区间;
,求函数h(x)的单调区间;
(2)若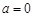 时函数h(x)有两个不同的零点x1,x2.
时函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;②求证: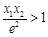 .
.
(本小题满分16分) 已知椭圆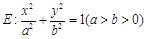 过点
过点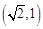 ,离心率为
,离心率为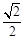 .
.
(1)若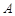 是椭圆
是椭圆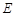 的上顶点,
的上顶点,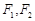 分别是左右焦点,直线
分别是左右焦点,直线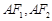 分别交椭圆于
分别交椭圆于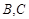 ,直线
,直线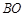 交
交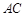 于D,求证
于D,求证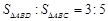 ;
;
(2)若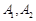 分别是椭圆
分别是椭圆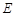 的左右顶点,动点
的左右顶点,动点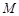 满足
满足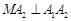 ,且
,且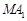 交椭圆
交椭圆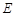 于点
于点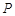 .
.
求证: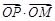 为定值.
为定值.