(本题6分)设全集为R, ,
, ,求
,求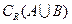 及
及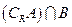
在四棱锥 中,底面
中,底面 是边长为
是边长为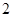 的菱形,
的菱形, ,
,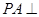 面
面 ,
, ,
,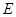 ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证: 面
面 ;
;
(2)求二面角 的大小的正弦值;
的大小的正弦值;
(3)求点 到面
到面 的距离.
的距离.
在 中,角
中,角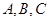 所对的边为
所对的边为 .已知
.已知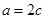 ,且
,且 .
.
(1)求 的值;
的值;
(2)当 时,求
时,求 的面积
的面积 .
.
设 为等差数列
为等差数列 的前
的前 项和,已知
项和,已知 .
.
(1)求数列 的通项公式
的通项公式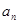 ;
;
(2)求证: 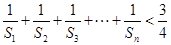 .
.
己知圆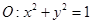 和直线
和直线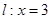 ,在
,在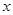 轴上有一点
轴上有一点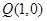 ,在圆
,在圆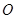 上有不与
上有不与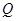 重合的两动点
重合的两动点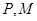 ,设直线
,设直线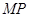 斜率为
斜率为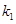 ,直线
,直线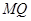 斜率为
斜率为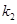 ,直线
,直线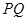 斜率为
斜率为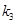 ,
,
(l)若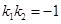
①求出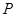 点坐标;
点坐标;
②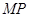 交
交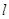 于
于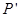 ,
,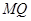 交
交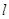 于
于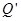 ,求证:以
,求证:以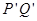 为直径的圆,总过定点,并求出定点坐标.
为直径的圆,总过定点,并求出定点坐标.
(2)若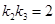 :判断直线
:判断直线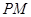 是否经过定点,若有,求出来,若没有,请说明理由.
是否经过定点,若有,求出来,若没有,请说明理由.
已知点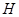 是
是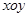 直角坐标平面上一动点,
直角坐标平面上一动点,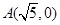 ,
,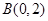 ,
,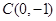 是平面上的定点:
是平面上的定点:
(1)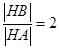 时,求
时,求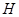 的轨迹方程;
的轨迹方程;
(2)当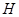 在线段
在线段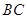 上移动,求
上移动,求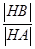 的最大值及
的最大值及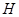 点坐标.
点坐标.