(本小题满分12分)一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。
(1)若从袋子里一次随机取出3个球,求得4分的概率;
(2)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分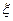 的概率分布列及数学期望。
的概率分布列及数学期望。
【2015高考天津,理18】(本小题满分13分)已知数列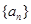 满足
满足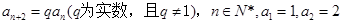 ,且
,且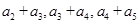 成等差数列.
成等差数列.
(Ⅰ)求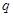 的值和
的值和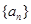 的通项公式;
的通项公式;
(Ⅱ)设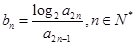 ,求数列
,求数列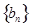 的前
的前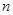 项和.
项和.
【2015高考安徽,理18】设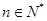 ,
,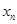 是曲线
是曲线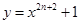 在点
在点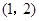 处的切线与x轴交点的横坐标.
处的切线与x轴交点的横坐标.
(Ⅰ)求数列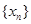 的通项公式;
的通项公式;
(Ⅱ)记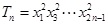 ,证明
,证明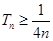 .
.
【2015高考山东,理18】设数列 的前n项和为
的前n项和为 .已知
.已知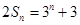 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足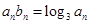 ,求
,求 的前n项和
的前n项和 .
.
【2015高考浙江,理20】已知数列 满足
满足 =
= 且
且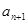 =
= -
-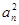 (
(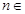
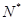 )
)
(1)证明:1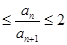 (
(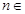
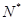 );
);
(2)设数列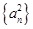 的前
的前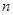 项和为
项和为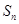 ,证明
,证明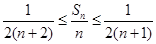 (
(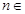
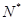 ).
).
【2015江苏高考,20】(本小题满分16分)设 是各项为正数且公差为d
是各项为正数且公差为d 的等差数列
的等差数列
(1)证明: 依次成等比数列;
依次成等比数列;
(2)是否存在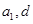 ,使得
,使得 依次成等比数列,并说明理由;
依次成等比数列,并说明理由;
(3)是否存在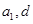 及正整数
及正整数 ,使得
,使得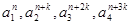 依次成等比数列,并说明理由.
依次成等比数列,并说明理由.