如图1所示,传送带保持1m/s的速度顺时针转动,现将一质量m=0.5kg的物体轻轻地放在传送带的A点上,设物体与传送带的动摩擦因u=0.1,A\B间的距离L=2.5m,则物体从A点运动到B点所经历的时间为(g取10m/s2) ( )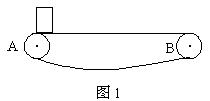
A.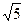 s s |
B.(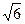 -1)s -1)s |
C.3s | D.2.5s |
如图所示,在匀强电场中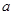 、
、 、
、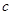 、
、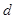 为矩形的四个顶点,
为矩形的四个顶点,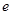 、
、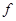 分别为
分别为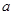
 边和
边和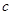
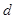 的中点且
的中点且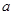
 长为
长为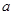
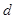 长的2倍。已知电场线的方向平行于矩形所在平面,
长的2倍。已知电场线的方向平行于矩形所在平面,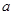 、
、 、
、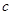 三点电势分别为4V、8V、6V,则:
三点电势分别为4V、8V、6V,则: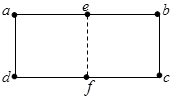
A.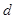 点的电势为2V 点的电势为2V |
B.电场线方向垂直于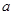 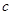 向下 向下 |
C.电场线方向垂直于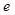 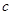 向下 向下 |
| D.一电子从a点运动到c点,电势能减少 |
如图为一列沿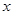 轴正方向传播的简谐横波在
轴正方向传播的简谐横波在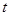 时刻的波形图及传播的距离,已知该波的周期为
时刻的波形图及传播的距离,已知该波的周期为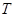 ,
,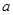 、
、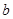 、
、 、
、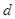 为沿波传播方向上的四个质点,下列判断正确的是:
为沿波传播方向上的四个质点,下列判断正确的是: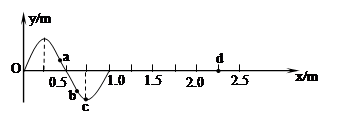
A.在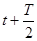 时刻, 时刻, 质点的速度达到最大 质点的速度达到最大 |
B.从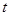 时刻起,质点 时刻起,质点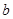 比质点 比质点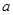 先回到平衡位置 先回到平衡位置 |
C.在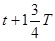 时刻, 时刻,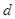 质点的速度向上且达到最大 质点的速度向上且达到最大 |
D.从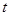 时刻起,在一个周期内, 时刻起,在一个周期内,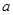 、 、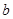 、 、 三个质点所通过的路程均为一个波长 三个质点所通过的路程均为一个波长 |
某物体运动的v-t图象如图所示,下列说法正确的是: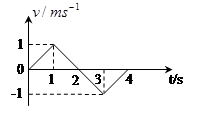
| A.物体在第1 s末运动方向发生变化 |
| B.前4s内合外力冲量为零 |
| C.第1s内合外力的功率保持不变 |
| D.前3s内合外力做正功 |
物体在万有引力场中具有的势能叫做引力势能。若取两物体相距无穷远时的引力势能为零,一个质量为m0的质点到质量为M0的引力源中心的距离为r0时,其万有引力势能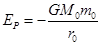 (式中G为引力常数)。一颗质量为m的人造地球卫星以半径为r1的圆形轨道环绕地球匀速飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为:(假设卫星的质量始终不变,不计空气阻力及其它星体的影响):
(式中G为引力常数)。一颗质量为m的人造地球卫星以半径为r1的圆形轨道环绕地球匀速飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为:(假设卫星的质量始终不变,不计空气阻力及其它星体的影响):
A.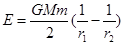 |
B.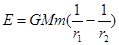 |
C.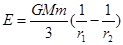 |
D.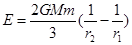 |
如图所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏上ab之间形成一条彩色光带.下面的说法中正确的是: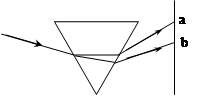
| A.a侧是红色光,b侧是紫色光 |
| B.通过同一双缝干涉装置,a侧光所形成的干涉条纹间距比b侧光的大 |
| C.若b侧光的光子能使某一金属发生光电效应,则a侧光的光子也一定能使其发生光电效应 |
| D.在三棱镜中a侧光的传播速率大于b侧光的传播速率 |