(本小题满分12分)已知数列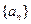 满足
满足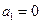 ,
,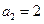 ,且对任意
,且对任意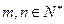 都有
都有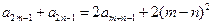
(Ⅰ)求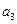 ,
,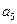 ;
;
(Ⅱ)设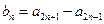
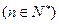 ,证明:
,证明: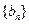 是等差数列;
是等差数列;
(Ⅲ)设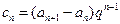
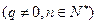 ,求数列
,求数列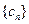 的前n项和
的前n项和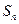 .
.
(本小题满分12分)在△ABC中,已知内角A、B、C所对的边分别为a、b、c,
且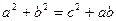
(1) 若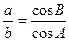 ,且
,且 ,求
,求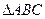 的面积;
的面积;
(2)已知向量 ,
, ,求|
,求| |的取值范围.
|的取值范围.
某市为了争创“全国文明城市”,市文明委组织了精神文明建设知识竞赛。 统计局调查中心随机抽取了甲、乙两队中各6名组员的成绩,得分情况如下表所示:
| 甲组 |
84 |
85 |
87 |
88 |
88 |
90 |
| 乙组 |
82 |
86 |
87 |
88 |
89 |
90 |
根据表中的数据,哪个组对精神文明建设知识的掌握更为稳定?
用简单随机抽样方法从乙组6名成员中抽取两名,他们的得分情况组成一个样本,求抽出的两名成员的分数差值至少是4分的概率。
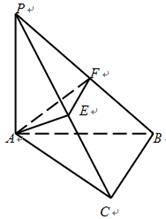
如图,几何体中,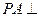 平面
平面 ,
, ,
,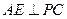 于点
于点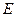 ,
, 于点
于点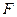 .
.
①若 ,求直线
,求直线 与平面
与平面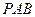 所成角的大小;
所成角的大小;
②求证: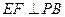 .
.
从圆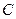 :
: 外一动点
外一动点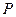 向圆
向圆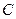 引一条切线,切点为
引一条切线,切点为 ,且
,且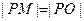 (
(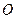 为坐标原点),求
为坐标原点),求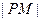 的最小值和
的最小值和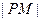 取得最小值时点
取得最小值时点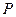 的坐标.
的坐标.
已知直线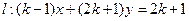 和圆
和圆 :
: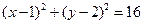 .
.
①求证:无论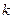 取何值,直线
取何值,直线 与圆
与圆 都相交;
都相交;
②求直线 被圆
被圆 截得的弦长的最小值和弦长取得最小值时实数
截得的弦长的最小值和弦长取得最小值时实数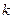 的值.
的值.