在空间中,有下列命题:①若直线a,b与直线c所成的角相等,则a∥b;②若直线a,b与平面a所成的角相等,则a∥b;③若直线a上有两点到平面a的距离相等,则a∥a;④若平面b上有不在同一直线上的三个点到平面a的距离相等,则a∥b.
则正确命题的个数是( )
| A. 0 | B. 1 | C. 2 | D. 3 |
给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b =c+d
=c+d ⇒a=c,b=d”;
⇒a=c,b=d”;
③“若a,b∈R,则a-b>0⇒a>b”类比推出“若a,b∈C,则a-b>0⇒a>b”.
其中类比得到的结论正确的个数是 ().
| A.0 | B.1 | C.2 | D.3 |
下列推理是归纳推理的是().
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜出椭圆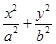 =1的面积S=πab =1的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
| 认为作业多 |
认为作业不多 |
总数 |
|
| 喜欢玩电脑游戏 |
18 |
9 |
27 |
| 不喜欢玩电脑游戏 |
8 |
15 |
23 |
| 总数 |
26 |
24 |
50 |
算得 .
.
附表:
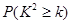 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
10.828 |
参照附表,得到的正确结论是()
A.有 的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
B.有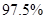 的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
C.在犯错误的概率不超过 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
D.在犯错误的概率不超过 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
已知y与x线性相关,其回归直线的斜率的估计值为1.23,样本的中心点为(4,5),则其回归直线方程为()
A.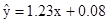 |
B.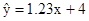 |
C.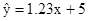 |
D.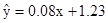 |
如果(3+i) z =10i(其中 ),则复数z的共轭复数为()
),则复数z的共轭复数为()
| A.-1+3i | B.1-3i | C.1+3i | D.-1-3i |