通过研究学生的学习行为,专家发现,学生的注意力随老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设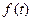 表示学生的注意力随时间
表示学生的注意力随时间 (分钟)的变化规律(注:
(分钟)的变化规律(注: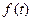 越大,表明学生的注意力越集中),经过实验分析得知:
越大,表明学生的注意力越集中),经过实验分析得知: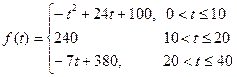 .
.
(1).讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2).讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3).一道数学难题需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
已知函数 图像上一点
图像上一点 处的切线方程为
处的切线方程为 (1)求
(1)求 的值;(2)若方程
的值;(2)若方程 在区间
在区间 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令 如果
如果 的图像与
的图像与 轴交于
轴交于 两点,
两点, 的中点为
的中点为 ,求证:
,求证:
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点. 
(1)若直线PQ过定点 ,求点A的坐标;
,求点A的坐标;
(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.
如图,在直角梯形ABCP中, ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.
某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的被淘汰.若有500人参加测试,学生成绩的频率分布直方图如图.
(1)求获得参赛资格的人数;
(2)根据频率直方图,估算这500名学生测试的平均成绩;
(3)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响.已知他连续两次答错的概率为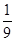 ,求甲在初赛中答题个数
,求甲在初赛中答题个数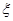 的分布列及数学期望
的分布列及数学期望 .
.
已知函数
(1)求函数 的最大值,并写出
的最大值,并写出 取最大值
取最大值 时的取值集合;
时的取值集合;
(2)在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值.