设函数 ,
,
(1)令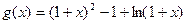 ,判断并证明
,判断并证明 在
在 上的单调性,并求
上的单调性,并求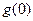 ;
;
(2)求函数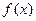 的最小值;
的最小值;
(3)是否存在实数m,n,满足-1<m<n,使得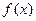 在区间[m,n]上的值域也为[m,n]。
在区间[m,n]上的值域也为[m,n]。
如图,长方体 中,
中, ,点
,点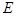 是
是 的中点.
的中点.
(1)求三棱锥 的体积;
的体积;
(2)证明: ;
;
(3)求二面角 的正切值.
的正切值.
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.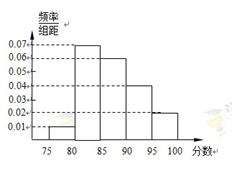
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
② 学校决定在这6名学生中随机抽取2名学生接受考官的面试,设第4组中有X名学生被考官面试,求X的分布列和数学期望.
已知函数 (
( ),其图象相邻两条对称轴之间的距离等于
),其图象相邻两条对称轴之间的距离等于 .
.
(1)求 的值;
的值;
(2)当 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 值.
值.
已知函数 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 在区间
在区间 上的最大值为12.
上的最大值为12.
(1)求 的解析式;
的解析式;
(2)设函数 在
在 上的最小值为
上的最小值为 ,求
,求 的表达式.
的表达式.
已知函数 的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
(1) 求 的解析式;
的解析式;
(2) 若 ,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.