某运动物体做直线运动,第1s内的平均速度是3m/s,第2s、第3s内的平均速度是6m/s,第4s内的平均速度是5m/s,则4s内运动物体的平均速度是多少?
如图所示,竖直平面内有足够长的金属导轨,轨距0.2m,金属导体棒ab可在导轨上无摩擦地上下滑动,ab的电阻为0.4Ω,导轨电阻不计,导体棒ab的质量为0.4g,垂直纸面向里的匀强磁场的磁应强度为0.2T,且磁场区域足够大,当ab导体棒自由下落0.4s时,突然接通电键K,求: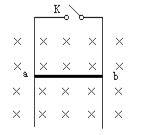
(1)K接通的瞬间,ab导体棒的加速度;
(2)ab导体棒匀速下落的速度是多少?(g取10m/s2)
如图所示的电路中,R1=3 Ω,R2=6 Ω,R3=1.5 Ω,C=20 μF,当开关S断开时,电源的总功率为2 W;当开关S闭合时,电源的总功率为4 W,求:
(1)电源的电动势和内电阻;
(2)闭合S时,电源的输出功率;
(3)S断开时,电容器所带的电荷量是多少?
如图甲所示,在磁感应强度为B的水平匀强磁场中,有两根竖直放置相距为L平行光滑的金属导轨,顶端用一阻直为R的电阻相连,两导轨所在的竖直平面与磁场方向垂直。一根质量为m的金属棒从静止开始沿导轨竖直向下运动,当金属棒下落龙时,速度达到最大,整个过程中金属棒与导轨保持垂直且接触良好。重力加速度为g,导轨与金属棒的电阻可忽略不计,设导轨足够长。求:
(l)通过电阻R的最大电流;
(2)从开始到速度最大过程中,金属棒克服安培力做的功WA;
(3)若用电容为C的平行板电容器代替电阻R,如图乙所示,仍将金属棒从静止释放,经历时间t的瞬时速度v1。
如图所示,在石轴上方存在匀强磁场,磁感应强度为B,方向垂直纸面向内。在x轴下方存在匀强电场,方向竖直向上。一个质量为m,电荷量为q,重力不计的带正电粒子从y轴上的a(h、0)点沿y正方向以某初速度开始运动,一段时间后,粒子与x轴正方向成45°进入电场,再次经过y轴的b点时速度方向恰好与y轴垂直。求:
(1)粒子在磁场中运动的轨道半径厂和速度大小v1;
(2)匀强电场的电场强度大小E;
(3)粒子从开始到第三欢经过x轴的时间t总
如图甲所示,质量m="l" kg的物块在平行斜面向上的拉力尸作用下从静止开始沿斜面向上运动,t=0.5s时撤去拉力,利用速度传感器得到其速度随时间的变化关系图象(v-t图象)如图乙所示,g取l0m/s2,求:
(1)2s内物块的位移大小s和通过的路程L;
(2)沿斜面向上运动两个阶段加速度大小a1、a2和拉力大小F。