已知角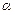 的顶点在原点,始边与
的顶点在原点,始边与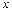 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点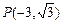 .
.
(1)求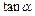 的值;
的值;
(2)定义行列式运算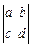
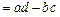 ,求行列式
,求行列式 的值;
的值;
(3)若函数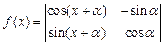 (
( ),求函数
),求函数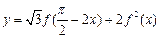 的最大值,并指出取到最大值时
的最大值,并指出取到最大值时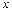 的值.
的值.
在一种智力有奖竞猜游戏中,每个参加者可以回答两个问题(题1和题2),且对两个问题可以按自己选择的顺序进行作答,但是只有答对了第一个问题之后才能回答第二个问题。假设:答对题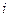 (
( ),就得到奖金
),就得到奖金 元,且答对题
元,且答对题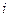 的概率为
的概率为 (
( ),并且两次作答不会相互影响.
),并且两次作答不会相互影响.
(I)当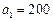 元,
元,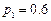 ,
,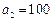 元,
元, 时,某人选择先回答题1,设获得奖金为
时,某人选择先回答题1,设获得奖金为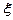 ,求
,求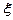 的分布列和
的分布列和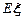 ;
;
(II)若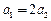 ,
, ,试问:选择先回答哪个问题时可能得到的奖金更多?
,试问:选择先回答哪个问题时可能得到的奖金更多?
△ABC中,已知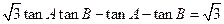 ,记角A,B,C的对边依次为
,记角A,B,C的对边依次为 .
.
(1)求∠C的大小;(2)若 ,且△ABC是锐角三角形,求
,且△ABC是锐角三角形,求 的取值范围.
的取值范围.
(15 分)
已知函数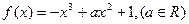
(1)若在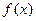 的图象上横坐标为
的图象上横坐标为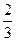 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若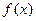 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数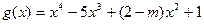 的图象与函数
的图象与函数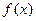 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
如图,设抛物线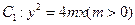 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以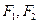 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线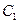 在
在 轴上方的交点为
轴上方的交点为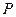 ,延长
,延长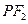 交抛物线于点
交抛物线于点 ,
, 是抛物线
是抛物线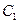 上一动点,且M在
上一动点,且M在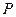 与
与 之间运动.
之间运动.
(1)当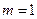 时,求椭圆
时,求椭圆 的方程;
的方程;
(2)当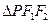 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.
(14 分)
从甲地到乙地一天共有A、B 两班车,由于雨雪天气的影响,一段时间内A 班车正点到达乙地的概率为0.7,B 班车正点到达乙地的概率为0.75。
(1)有三位游客分别乘坐三天的A 班车,从甲地到乙地,求其中恰有两名游客正点到达的概率
(答案用数字表示)。
(2)有两位游客分别乘坐A、B 班车,从甲地到乙地,求其中至少有1 人正点到达的概率
(答案用数字表示)。