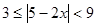已知函数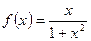 .
.
(1)证明函数具有奇偶性;
(2)证明函数在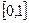 上是单调函数;
上是单调函数;
(3)求函数在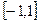 上的最值.
上的最值.
已知函数
(1)求证: 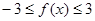
(2)求不等式  的解集
的解集
在雅安发生地震灾害之后,救灾指挥部决定建造一批简易房,供灾区群众临时居住,房形为长方体,高2.5米,前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即钢板的高均为2.5米,用长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元,房顶用其他材料建造,每平方米材料费为200元,每套房材料费控制在32000元以内。
(1)设房前面墙的长为 ,两侧墙的长为
,两侧墙的长为 ,一套简易房所用材料费为p,试用
,一套简易房所用材料费为p,试用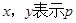 。
。
(2)一套简易房面积S的最大值是多少?当S最大时,前面墙的长度是多少?
设 ,用反证法证明:
,用反证法证明: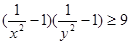
求证: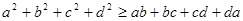
解不等式