(本小题满分12分)
某班全部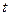 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是 按上述分组方式得到的频率分布表。
按上述分组方式得到的频率分布表。
| 分 组 |
频数 |
频率 |
| [13,14) |
 |
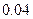 |
| [14,15) |
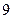 |
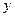 |
| [15,16) |
 |
 |
| [16,17) |
 |
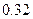 |
| [17,18] |
 |
 |
(1)求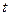 及上表中的
及上表中的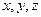 的值;
的值;
(2)设m,n是从第一组或第五组中任意抽取的两名学生的 百米测试成绩,求事件“
百米测试成绩,求事件“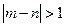 ”的
”的 概率.
概率.
两个盒内分别盛着写有0,1,2,3,4,5六个数字的六张卡片,若从每盒中各取一张,求所取两数之和等于6的概率,现有甲、乙两人分别给出的一种解法:
甲的解法:因为两数之和可有0,1,2,…,10共11种不同的结果,所以所求概率为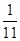 .
.
乙的解法:从每盒中各取一张卡片,共有36种取法,其中和为6的情况有5种:(1,5)、(5,1)、(2,4)、(4,2)、(3,3)因此所求概率为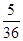 .
.
试问哪一种解法正确?为什么?
在一次口试中,要从5道题中随机抽出3道进行回答,答对其中的2道题就获得优秀,答对其中的1道题就获得及格,某考生会回答5道题中的2道题,试求:
(1)他获得优秀的概率是多少?
(2)他获得及格与及格以上的概率是多大?
一个口袋内装有5个白球和3个黑球,从中任意取出一个球.
(1)“取出的球是红球”是什么事件,它的概率是多少?
(2)“取出的球是黑球”是什么事件,它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件,它的概率是多少?
做A、B、C三件事的费用各不相同.在一次游戏中,要求参加者写出做这三件事所需费用的顺序(由多到少排列),如果某个参加者随意写出答案,他正好答对的概率是多少?
甲盒中有红、黑、白三种颜色的球各3个,乙盒中有黄、黑、白三种颜色球各2个,从两个盒子中各取1个球
⑴求取出的两个球是不同颜色球的概率
⑵请设计一个随机模拟的方法来模拟⑴中的问题