投资生产A产品时，每生产100吨需要资金200万元，需场地200m2，可获利润300万元，投资生产B产品时，每生产100吨需资金300万元，需场地100m2，可获利润200万元，某单位有可使用资金1400万元，场地900 m2，问作怎样的组合可获利最多？最多利润是多少？
| |
资金（万元） |
场地（m2） |
利润（万元） |
| A产品（每百吨） |
200 |
200 |
300 |
| B产品（每百吨） |
300 |
100 |
200 |
已知
，数列
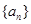的首项
（1）求数列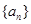的通项公式；
（2）设
，数列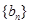
的前n项和为
，求使
的最小正整数n。
设函数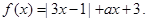
（1）若a=1，解不等式
；
（2）若函数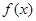
有最小值，求实数a的取值范围。
已知曲线C1的极坐标方程为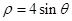
，曲线C2的极坐标方程为
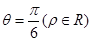，曲线C1，C2相交于点M，N。
（1）将曲线C1，C2的极坐标方程化为直角坐标方程；
（2）求线段MN的长。
如图，已知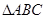
中，AB=BC，以AB为直径的⊙O交AC于点D，过D作
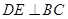，垂足为E，连结OE。若
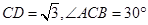，分别求AB，OE的长。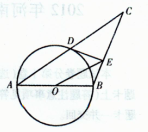
对于集合M，定义函数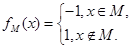
对于两个集合M，N，定义集合
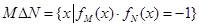. 已知A={2，4，6，8，10}，B={1，2，4，8，16}.
（Ⅰ）写出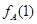
和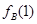
的值，并用列举法写出集合
；
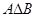（Ⅱ）用Card(M)表示有限集合M所含元素的个数.
（ⅰ）求证：当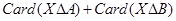
取得最小值时， 
；
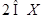（ⅱ）求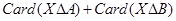的最小值