(本小题8分)
设函数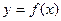 是定义域在
是定义域在 的函数,且
的函数,且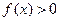 ,对于任意的实数
,对于任意的实数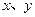 ,都有
,都有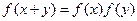 ,当
,当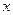 >0时,
>0时, .
.
(1)求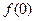 的值;
的值;
(2)判断函数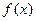 在
在 的单调性并用定义证明;
的单调性并用定义证明;
(3)若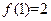 ,解不等式
,解不等式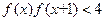 .
.
已知棱长为1的正方体AC1,E、F分别是B1C1、C1D的中点.
(1)求点A1到平面的BDEF的距离;
(2)求直线A1D与平面BDEF所成的角.
已知在 的展开式中,第6项
的展开式中,第6项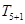 为常数项.
为常数项.
(1)求n;
(2)问展开式中的有理项.分别为第几项?说明理由。
7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?(用数字作答)
(1)两名女生必须相邻而站;
(2)4名男生互不相邻.
已知函数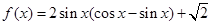 ,
,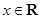 .
.
(1)求函数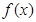 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)求函数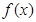 在区间
在区间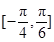 上的最小值和最大值;
上的最小值和最大值;
(3)若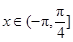 ,求使
,求使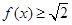 的
的 取值范围.
取值范围.
如下图,在平面直角坐标系中,锐角 和钝角
和钝角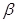 的终边分别与单位圆交于
的终边分别与单位圆交于 两点.
两点.
(1)若 两点的纵坐标分别为
两点的纵坐标分别为 ,求
,求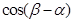 的值;
的值;
(2)已知点 是单位圆上的一点,且
是单位圆上的一点,且 ,求
,求 和
和 的夹角
的夹角 .
.