(本小题12分)
已知
,
(1)判断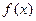
的奇偶性并用定义证明；
(2)当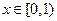
时，总有
成立，求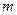
的取值范围.
已知函数
，a＞0，
（Ⅰ）讨论
的单调性；
（Ⅱ）设a=3，求在区间{1，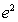
}上值域。期中e=2.71828…是自然对数的底数。
首项为正数的数列{
}满足
.
(Ⅰ)证明：若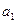
为奇数，则对一切
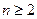，都是奇数；
(Ⅱ)若对一切
，都有
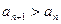，求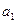的取值范围。
点P（x0,y0）在椭圆
1(a>b>0)上，x0=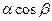
, y0=
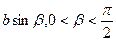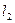. 直线
与直线
：
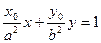垂直，O为坐标原点，直线OP的倾斜角为
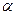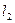，直线的倾斜角为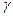
.
（Ⅰ）证明：点P是椭圆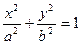
与直线的唯一交点；
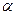（Ⅱ）证明：tan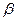,tan
,tan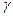构成等比数列。
已知函数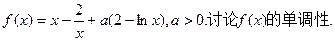
如图，四棱椎 的底面 是菱形，其对角线 都与平面 垂直， , .
(Ⅰ) 求二面角
的大小；
(Ⅱ) 求四棱锥
与四棱锥
公共部分的体积。 
