(本题满分14分)
已知函数 ,
,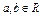 ,
,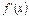 是函数
是函数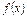 的导函数.
的导函数.
(I)若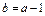 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(II)若 ,
,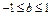 ,求方程
,求方程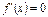 有实数根的概率.
有实数根的概率.
如图, 已知底角为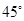 的等腰梯形
的等腰梯形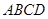 , 底边
, 底边 长为
长为 , 腰长为
, 腰长为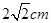 , 当一条垂直于底边
, 当一条垂直于底边 的直线
的直线 从左至右移动(与梯形
从左至右移动(与梯形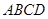 有公共点)时, 直线
有公共点)时, 直线 把梯形分成两部分, 令
把梯形分成两部分, 令 , 试写出左边部分的面积
, 试写出左边部分的面积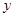 与
与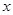 的函数解析式, 并画出大致图象.
的函数解析式, 并画出大致图象.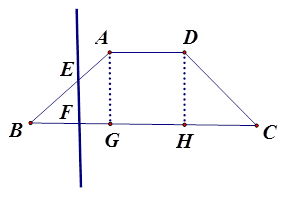
(本小题满分8分)已知函数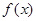 在其定义域
在其定义域 时单调递增, 且对任意的
时单调递增, 且对任意的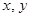
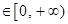 都有
都有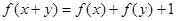 成立,且
成立,且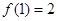 ,
,
(1)求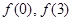 的值;
的值;
(2)解不等式: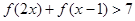 .
.
(本小题满分8分)
已知函数
(1)求实数 的取值范围,使函数
的取值范围,使函数 在区间
在区间 上是单调函数;
上是单调函数;
(2)若 , 记
, 记 的最大值为
的最大值为 , 求
, 求 的表达式并判断其奇偶性.
的表达式并判断其奇偶性.
(本小题满分8分)(1)解含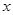 的不等式:
的不等式: 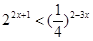 ;
;
(2)求函数 的值域, 并写出其单调区间.
的值域, 并写出其单调区间.
(本小题满分8分)已知集合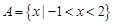 ,集合
,集合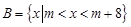 .
.
(1)若 ,求实数
,求实数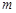 的取值范围;
的取值范围;
(2)若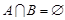 ,求实数
,求实数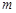 的取值范围.
的取值范围.