(本小题满分12分)
已知椭圆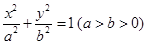 的长轴长为
的长轴长为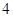 ,且点
,且点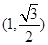 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点的直线 交椭圆于
交椭圆于 两点,若以
两点,若以 为直径的圆过原点,
为直径的圆过原点,
求直线 方程.
方程.
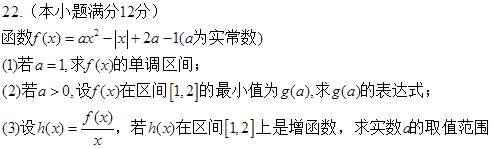
.(本小题满分12分)
如图,在正方体 中,E、F分别是中点。
中,E、F分别是中点。
(Ⅰ)求证: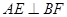 ;
;
(Ⅱ)求证: ;
;
(III)棱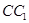 上是否存在点P使
上是否存在点P使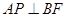 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。
.(本小题满分12分)
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
.(本小题满分12分)
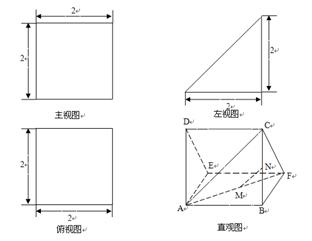
如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点。
(Ⅰ)求证:MN∥平面CDEF;
(Ⅱ)求多面体A-CDEF的体积;
(Ⅲ)求证: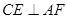 。
。