.(本小题满分12分)
如图,在正方体 中,E、F分别是中点。
中,E、F分别是中点。
(Ⅰ)求证: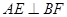 ;
;
(Ⅱ)求证: ;
;
(III)棱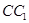 上是否存在点P使
上是否存在点P使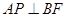 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,且
,且 。
。
(1)求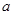 的值,(2)求
的值,(2)求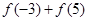 的值.
的值.
已知命题p:“ x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“ x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
已知全集 R,
R, ,
, .
.
(1)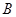

 ;
;
(2)若不等式 的解集为
的解集为 ,求
,求 、
、 的值
的值
设函数f(x)=lnx-ax+ -1.
-1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0<a< 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;
(3) 当a= 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-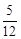 , 若对于
, 若对于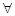 x1∈
x1∈ ,
, 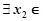 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<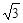 +1).
+1).
已知点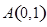 、
、 ,
, 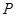 是一个动点, 且直线
是一个动点, 且直线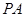 、
、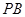 的斜率之积为
的斜率之积为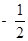 .
.
(1) 求动点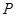 的轨迹
的轨迹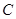 的方程;
的方程;
(2) 设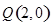 , 过点
, 过点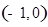 的直线
的直线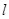 交
交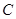 于
于 、
、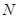 两点, 若对满足条件的任意直线
两点, 若对满足条件的任意直线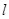 , 不等式
, 不等式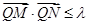 恒成立, 求
恒成立, 求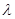 的最小值.
的最小值.