(本小题满分12分)
设数列 的前
的前 项和为
项和为 ,已知
,已知
(1)设 ,证明数列
,证明数列 是等比数列;
是等比数列;
(2)求数列 的通项公式.
的通项公式.
设函数 ,其中
,其中
(1)讨论 在其定义域上的单调性;
在其定义域上的单调性;
(2)当 时,求
时,求 取得最大值和最小值时的
取得最大值和最小值时的 的值.
的值.
设椭圆E的方程为 点O为坐标原点,点A的坐标为
点O为坐标原点,点A的坐标为 ,点B的坐标为(0,b),点M在线段AB上,满足
,点B的坐标为(0,b),点M在线段AB上,满足 直线OM的斜率为
直线OM的斜率为 .
.
(Ⅰ)求E的离心率e;
(Ⅱ)设点C的坐标为(0,-b),N为线段AC的中点,证明:MN AB.
AB.
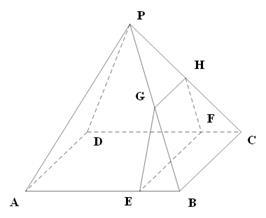
如图,四棱锥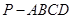 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为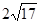 .点
.点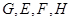 分别是棱
分别是棱 上共面的四点,平面
上共面的四点,平面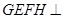 平面
平面 ,
,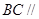 平面
平面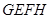 .
.
(1)证明:
(2)若 ,求四边形
,求四边形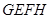 的面积.
的面积.
为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下: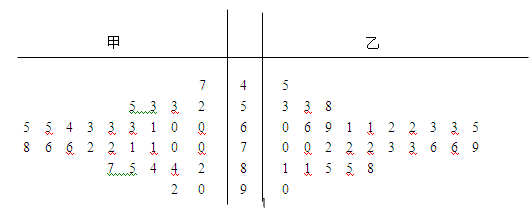
(Ⅰ)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(Ⅱ)设甲、乙两校高三年级学生这次联考数学平均成绩分别为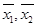 ,估计
,估计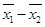 的值.
的值.
设数列 满足
满足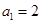 ,
,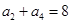 ,且对任意
,且对任意 ,函数
,函数  满足
满足
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和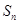 .
.