(7分) 已知两条直线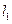 :
: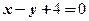 与
与 :
: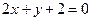 的交点
的交点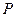 ,求满足下列条件的直线方程
,求满足下列条件的直线方程
(1)过点P且过原点的直线方程;
(2)过点P且平行于直线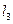 :
: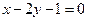 直线
直线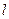 的方程;
的方程;
已知函数f(x)=|x+2|+|2x-4|
(1)求f(x)<6的解集;
(2)若关于 的不等式f(x)≥m2-3m的解集是R,求m的取值范围
的不等式f(x)≥m2-3m的解集是R,求m的取值范围
已知平面直角坐标系xOy,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为 ,曲线C的极坐标方程为
,曲线C的极坐标方程为
(Ⅰ)写出点P的直角坐标及曲线C的普通方程;
(Ⅱ)若 为C上的动点,求
为C上的动点,求 中点
中点 到直线
到直线 (t为参数)距离的最小值
(t为参数)距离的最小值
如图所示, 为圆
为圆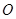 的切线,
的切线, 为切点,
为切点,
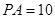 ,
,
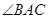 的角平分线与
的角平分线与 和圆
和圆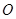 分别交于点
分别交于点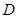 和
和
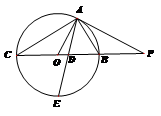
(1)求证 (2)求
(2)求 的值
的值
已知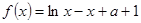
(1)若存在 使得
使得 ≥0成立,求
≥0成立,求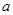 的范围
的范围
(2)求证:当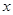 >1时,在(1)的条件下,
>1时,在(1)的条件下, 成立
成立
已知椭圆中心在原点,焦点在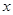 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
(1)求椭圆的方程;
(2)设直线 经过点
经过点 (0,1),且与椭圆交于
(0,1),且与椭圆交于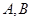 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.