已知椭圆中心在原点，焦点在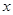
轴上，焦距为2，离心率为
（1）求椭圆的方程；
（2）设直线
经过点
（0,1），且与椭圆交于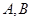
两点，若
，求直线的方程.
如图，正方形ABCD和三角形ACE所在的平面互相垂直，EF∥BD，AB＝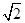
EF.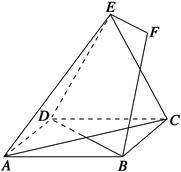
(1)求证：BF∥平面ACE；
(2)求证：BF⊥BD.
已知四棱锥PABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E，F分别为棱BC，AD的中点．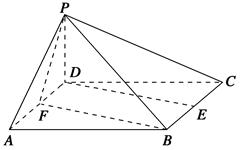
(1)求证：DE∥平面PFB；
(2)已知二面角PBFC的余弦值为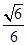
，求四棱锥PABCD的体积．
如图，四边形ABCD是边长为2的正方形，直线l与平面ABCD平行，E和F是l上的两个不同点，且EA＝ED，FB＝FC.E′和F′是平面ABCD内的两点，EE′和FF′都与平面ABCD垂直．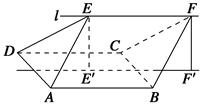
(1)证明：直线E′F′垂直且平分线段AD；
(2)若∠EAD＝∠EAB＝60 °，EF＝2.求多面体ABCDEF的体积．
已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为4的等腰三角形，侧视图是一个底边长为6、高为4的等腰三角形．
(1)求该几何体的体积V；
(2)求该几何体的侧面积S.
已知首项为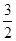
的等比数列{an}不是递减数列，其前n项和为Sn(n∈N*)，且S3＋a3，S5＋a5，S4＋a4成等差数列．
(1)求数列{an}的通项公式；
(2)设Tn＝Sn－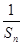
(n∈N*)，求数列{Tn}的最大项的值与最小项的值．