(本小题满分l4分)如图,边长为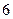 的正方体
的正方体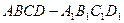 中,
中, 是
是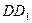 的中点,
的中点, 在线段
在线段 上,且
上,且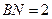 .
.
(1)求异面直线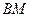 与
与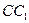 所成角的余弦值;
所成角的余弦值;
(2)证明: 面
面 ;
;
(3)求点 到面
到面 的距离.
的距离.
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
已知
(1)求 ;
;
(2)求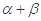 的值(其中
的值(其中 ).
).
函数 ,若不等式
,若不等式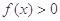 的解集为
的解集为 .(Ⅰ)求
.(Ⅰ)求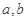 的值;(Ⅱ)若函数
的值;(Ⅱ)若函数 在
在 上的最小值为1,求实数
上的最小值为1,求实数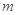 的值.
的值.
理科(本小题14分)已知函数 ,当
,当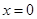 时,函数
时,函数 取得极大值.
取得极大值.
(Ⅰ)求实数 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数 在区间
在区间 内导数都存在,且
内导数都存在,且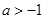 ,则存在
,则存在 ,使得
,使得 .试用这个结论证明:若
.试用这个结论证明:若 ,函数
,函数 ,则对任意
,则对任意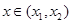 ,都有
,都有 ;(Ⅲ)已知正数
;(Ⅲ)已知正数 满足
满足 求证:当
求证:当 ,
,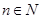 时,对任意大于
时,对任意大于 ,且互不相等的实数
,且互不相等的实数 ,都有
,都有
文科(本小题满分14分)设函数 。(Ⅰ)若函数
。(Ⅰ)若函数 在
在 处与直线
处与直线 相切,①求实数
相切,①求实数 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当 时,若不等式
时,若不等式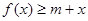 对所有的
对所有的 都成立,求实数m的取值范围。)
都成立,求实数m的取值范围。)