理科(本小题14分)已知函数 ,当
,当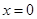 时,函数
时,函数 取得极大值.
取得极大值.
(Ⅰ)求实数 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数 在区间
在区间 内导数都存在,且
内导数都存在,且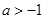 ,则存在
,则存在 ,使得
,使得 .试用这个结论证明:若
.试用这个结论证明:若 ,函数
,函数 ,则对任意
,则对任意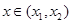 ,都有
,都有 ;(Ⅲ)已知正数
;(Ⅲ)已知正数 满足
满足 求证:当
求证:当 ,
,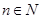 时,对任意大于
时,对任意大于 ,且互不相等的实数
,且互不相等的实数 ,都有
,都有
函数 是
是 的导函数.
的导函数.
(Ⅰ)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)若 的值.
的值.
(本小题满分14分)给定函数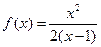
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足,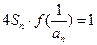 求证:
求证: ;
;
(3)设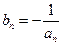 ,
,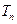 为数列
为数列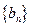 的前
的前 项和,求证:
项和,求证: 。
。
(本小题满分14分)如图,已知曲线 与曲线
与曲线 交于点
交于点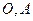 .直线
.直线 与曲线
与曲线 分别相交于点
分别相交于点 .
.
(Ⅰ)写出四边形 的面积
的面积 与
与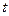 的函数关系
的函数关系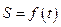 ;
;
(Ⅱ)讨论 的单调性,并求
的单调性,并求 的最大值.
的最大值.
(本小题满分14分)等比数列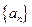 中,
中,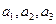 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且
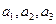 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 |
第二列 |
第三列 |
|
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ) 求数列
求数列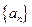 的通项公式;
的通项公式;
(Ⅱ)若数列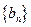 满足
满足 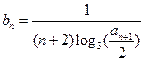 ,记数列
,记数列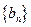 的前n项和为
的前n项和为 ,证明
,证明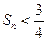
(本小题满分12分)如果直线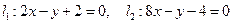 与
与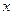 轴正半轴,
轴正半轴,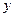 轴正半轴围成的四边形封闭区域(含边界)中的点,使函数
轴正半轴围成的四边形封闭区域(含边界)中的点,使函数 的最大值为8,求
的最大值为8,求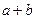 的最小值
的最小值