(本小题满分14分)
如图,在直四棱柱ABCD-A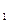 B
B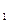 C
C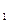 D
D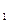 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
AA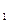 ="2, " E、E
="2, " E、E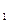 分别是棱AD、AA
分别是棱AD、AA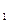 的中点.
的中点. 

(1)设F是棱AB的中点,证明:直线EE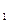 //平面FCC
//平面FCC ;
;
(2)证明:平面D1AC⊥平面BB1C1C.
已知圆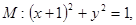 圆
圆 动圆
动圆 与圆
与圆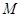 外切并与圆
外切并与圆 内切,圆心
内切,圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)求 的方程;
的方程;
(2)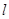 是与圆
是与圆 ,圆
,圆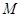 都相切的一条直线,
都相切的一条直线,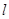 与曲线
与曲线 交于
交于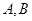 两点,当圆
两点,当圆 的半径最长时,求
的半径最长时,求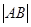 .
.
设等差数列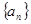 的前
的前 项和为
项和为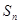 ,且
,且 ,
,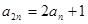 .
.
(1)求数列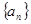 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,求
,求 的通项公式;
的通项公式;
(3)求数列 前
前 项和
项和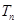 .
.
已知函数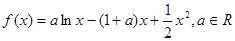
(1)讨论函数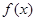 的单调区间;
的单调区间;
(2)已知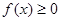 对定义域内的任意
对定义域内的任意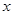 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,在四棱锥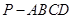 中,
中,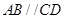 ,
, ,
, ,
,  ,
, ,
, 和
和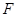 分别是
分别是 和
和 的中点.
的中点.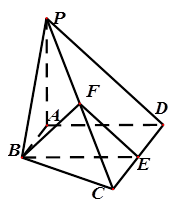
(1)求证:  底面
底面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求三棱锥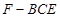 的体积.
的体积.
一次考试中,五名学生的数学、物理成绩如下表所示: 
(1)要从 5 名学生中选2 人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据的线性回归方程  .
.
(附:回归直线的方程是 :  , 其中
, 其中 )
)