(本小题满分12分)
已知直三棱柱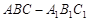 中,
中, ,
,  ,若
,若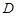 是
是 中点.
中点.
(Ⅰ)求证: ∥平面
∥平面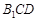 ;
;
(Ⅱ)求异面直线 和
和 所成的角.
所成的角.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(I)从袋中随机抽取一个球,将其编号记为 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为 .求关于
.求关于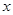 的一元二次方程
的一元二次方程 有实根的概率;
有实根的概率;
(II)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以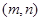 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域 内的概率.
内的概率.
如图,在四棱锥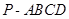 中,
中,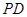 ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形,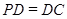 ,
,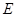 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: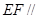 平面
平面 ;
;
(II)求证: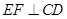 ;
;
(III)设PD="AD=a," 求三棱锥B-EFC的体积.
已知向量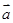 =(
=(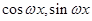 ),
),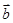 =(
=(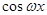 ,
,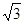
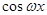 ),其中(
),其中(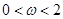 ).函数
).函数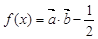 ,其图象的一条对称轴为
,其图象的一条对称轴为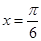 .
.
(I)求函数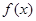 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若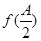 =1,b=l,S△ABC=
=1,b=l,S△ABC=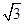 ,求a的值.
,求a的值.
已知曲线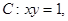 过
过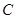 上一点
上一点 作一斜率为
作一斜率为 的直线交曲线
的直线交曲线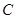 于另一点
于另一点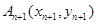 ,点列
,点列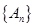 的横坐标构成数列
的横坐标构成数列 ,其中
,其中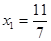 .
.
(I)求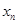 与
与 的关系式;
的关系式;
(II)令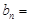
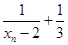 ,求证:数列
,求证:数列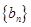 是等比数列;
是等比数列;
(III)若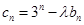 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立。
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立。
已知函数 的图象在点
的图象在点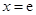 (
(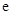 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.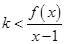 (Ⅰ)求实数
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若 ,且对任意
,且对任意 恒成立,求
恒成立,求 的最大值;
的最大值;
(Ⅲ)当 时,证明
时,证明 .
.