（本小题满分12分）如图四边形ABCD为菱形，G为AC与BD交点，
，
（1）证明：平面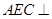
平面
；
（2）若
，
, 令AE与平面ABCD所成角为
, 且
, 求该四棱锥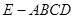
的体积．
（本小题满分12分）已知双曲线
, 若双曲线的渐近线过点
, 且双曲线过点
（1）求双曲线
的方程;
（2）若双曲线
的左、右顶点分别为
,点
在上且直线
的斜率的取值范围是
,求直线
斜率的取值范围．
（本小题满分10分）
（1）设函数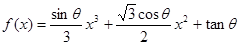
,其中θ∈
,求导数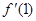
的取值范围;
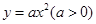（2）若曲线
与曲线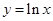
在它们的公共点
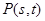处具有公共切线，
求公共切线的方程．
（本小题满分10分）设命题p：函数
的定义域为R, 命题q：双曲线
的离心率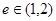
,
（1）如果p是真命题，求实数
的取值范围；
（2）如果命题“p或q”为真命题，且“p且q”为假命题，求实数的取值范围．
已知等差数列
满足
；数列
的前n项和为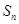
，且满足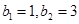
，
．
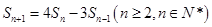（Ⅰ）分别求数列
的通项公式；
（Ⅱ）若对任意的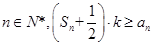
恒成立，求实数k的取值范围．
,直线
,过点
且与直线
相切的动圆圆心
的
.
的前
项和为
，且满足:点
.