已知函数 ,在
,在 轴右侧的第一个最高点的横标为
轴右侧的第一个最高点的横标为 .
.
(1)求 ;
;
(2)若将函数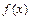 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数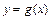 的图象,求函数
的图象,求函数 的最大值及单位递减区间.
的最大值及单位递减区间.
(本小题满分12分)已知函数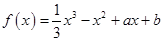 的图象在点P
的图象在点P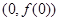 处的切线方程为
处的切线方程为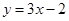 .
.
(Ⅰ)求实数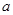 ,
, 的值;
的值;
(Ⅱ)设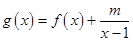 是[2,+
是[2,+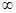 )上的增函数,求实数m的最大值.
)上的增函数,求实数m的最大值.
(本小题满分12分)已知椭圆

 过点M(0,2),离心率
过点M(0,2),离心率 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点N(2,0)的直线l与椭圆相交于A、B两点,且∠AOB为锐角(其中O为坐标原点),求直
线l斜率的取值范围.
(本小题满分12分)从某学校 的800名男生中随机抽取50名测量身高,被测学生身高全部介
于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165)……
第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部份,已知第一组与第八组人数
相同,第六组的人数为4人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,
,
事件 ,事件
,事件 ,求概率
,求概率 .
.
(本小题满分12分)如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA,AB=AD=DE= ,M是线段AE上的动点.
,M是线段AE上的动点.
(Ⅰ)试确定点M的位置,使AC//平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE—BCF分成的两部分的体积之比.
(本小题满分12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足 ,
, ·
· =3.
=3.
(Ⅰ)求△ABC的面积;
(Ⅱ)若b+c=6,求a的值.