(本小题满分12分)已知椭圆

 过点M(0,2),离心率
过点M(0,2),离心率 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点N(2,0)的直线l与椭圆相交于A、B两点,且∠AOB为锐角(其中O为坐标原点),求直
线l斜率的取值范围.
如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有多少种?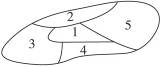
已知集合A={x| },B={x|
},B={x| },C={x|
},C={x| },全集U=A∪B∪C,现从U中每次取出2奇2偶四个数.
},全集U=A∪B∪C,现从U中每次取出2奇2偶四个数.
(1)能组成多少个无重复数字的四位奇数?
(2)能组成多少个被5除余2的数?
某市工商局对35种商品进行抽样检查,鉴定结果有15种假货,现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同的取法有多少种?
(2)其中某一种假货不能在内,不同的取法有多少种?
(3)恰有2种假货在内,不同的取法有多少种?
(4)至少有2种假货在内,不同的取法有多少种?
(5)至多有2种假货在内,不同的取法有多少种?
平面上有9个点,其中有4个点在同一条直线上,此外任三点不共线.
(1)过每两点连线,可得几条直线?
(2)以每三点为顶点作三角形,可作几个?
(3)以一点为端点,作过另一点的射线,这样的射线可作出几条?
某次足球赛共12支球队参加,分三个阶段进行:
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
问全部赛程共需比赛多少场?