(本小题10分)
对于函数f（x）（x
）恒有f（ab）=f（a）+f(b)且x＞1时f（x）＞0 ，f（2）=1
(1)求f（4）、f（1）、f（-1）的值；
(2)求证f（x）为偶函数；
(3)求证f（x）在（0，+
）上是增函数；
(4）解不等式f（x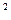
-5）＜2.
已知过点A（0，1）且斜率为k的直线l与圆C：(x-2)2+(y-3)2=1相交于M、N两点.
(1).求实数k的取值范围
(2).求证：
为定值
(3).若O为坐标原点，且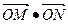
=12,求直线l的方程
如图， ABCD为矩形，CF⊥平面ABCD，DE⊥平面ABCD，AB=4a，BC= CF=2a，DE=a， P为AB的中点.
（1）求证：平面PCF⊥平面PDE；
（2）求证：AE∥平面BCF.
已知两个命题r(x):sinx+cosx>m;s(x):x2+mx+1>0.如果对于任意实数x，r(x)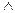
s(x) 为假，r(x)
s(x)为真，求实数m的取值范围。
已知双曲线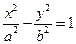
的离心率为2，焦点与椭圆
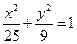的焦点相同，求双曲
线的方程及焦点坐标
分别举出一个全称命题和一个特称命题，并对此命题进行否定