(本小题满分14分)已知 c>0, 设命题p:指数函数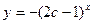 在实数集R上为增函数,命题q:不等式
在实数集R上为增函数,命题q:不等式 在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
如图,射线 、
、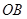 所在的直线的方向向量分别为
所在的直线的方向向量分别为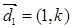 、
、 (
(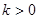 ),点
),点 在
在 内,
内, 于
于 ,
,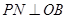 于
于 .
.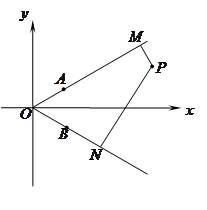
(1)若 ,
,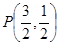 ,求
,求 的值;
的值;
(2)若 ,△
,△ 的面积为
的面积为 ,求
,求 的值;
的值;
(3)已知 为常数,
为常数, 、
、 的中点为
的中点为 ,且
,且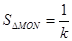 ,当
,当 变化时,求
变化时,求 的取值范围.
的取值范围.
已知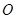 为
为 的外心,以线段
的外心,以线段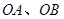 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为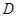 ,再以
,再以 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为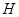 .
.
(1) 若 ,试用
,试用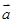 、
、 、
、 表示
表示 ;
;
(2) 证明: ;
;
(3) 若 的
的 ,
, ,外接圆的半径为
,外接圆的半径为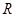 ,用
,用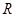 表示
表示 .
.
在直角坐标系中,已知两点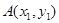 ,
,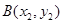 ;
;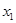 ,
,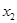 是一元二次方程
是一元二次方程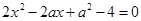 两个不等实根,且
两个不等实根,且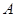 、
、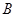 两点都在直线
两点都在直线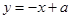 上.
上.
(1)求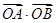 ;
;
(2) 为何值时
为何值时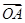 与
与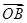 夹角为
夹角为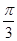 .
.
已知 的顶点
的顶点 ,
, 边上的中线所在的直线方程是
边上的中线所在的直线方程是 ,AC边上的高所在的直线方程是
,AC边上的高所在的直线方程是 .
.
求:(1)AC边所在的直线方程;
(2)AB边所在的直线方程.
中秋节前几天,小毛所在的班级筹划组织一次中秋班会,热心的小毛受班级同学委托,去一家小礼品店为班级的三个小组分别采购三种小礼物:中国结、记事本和笔袋(每种礼物的品种和单价都相同).
三个小组给他的采购计划各不相同,各种礼物的采购数量及价格如下表所示:
为了结账,小毛特意计算了各小组的采购总价(见上表合计栏),可是粗心的小毛却不慎抄错了其中一个数字.第二天,当他按照自己的记录去向各小组报销的时候,有同学很快发现其中有错.发现错误的同学并不知道三种小礼物的单价,那么他是如何作出判断的呢?请你用所学的行列式的知识对此加以说明.