(本题满分16分,第1小题5分,第2小题6分,第3小题5分)
已知函数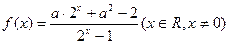 ,其中
,其中 为常数,且
为常数,且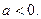
(1)若 是奇函数,求
是奇函数,求 的取值集合A;
的取值集合A;
(2)(理)当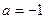 时,设
时,设 的反函数为
的反函数为 ,且函数
,且函数 的图像与
的图像与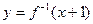 的图像关于
的图像关于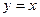 对称,求
对称,求 的取值集合B;
的取值集合B;
(文)当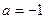 时,求
时,求 的反函数;
的反函数;
(3)(理)对于问题(1)(2)中的A、B,当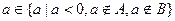
 时,不等式
时,不等式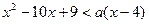 恒成立,求
恒成立,求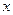 的取值范围。
的取值范围。
(文)对于问题(1)中的A,当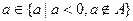 时,不等式
时,不等式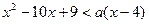 恒成立,求
恒成立,求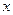 的取值范围。
的取值范围。
已知函数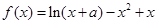 ,
, ,且
,且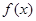 点
点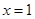 处取得极值.
处取得极值.
(Ⅰ)求实数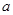 的值;
的值;
(Ⅱ)若关于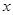 的方程
的方程 在区间
在区间 上有解,求
上有解,求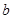 的取值范围;
的取值范围;
(Ⅲ)证明: .
.
已知椭圆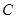 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆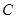 右焦点
右焦点 ,且
,且
(Ⅰ)求椭圆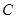 的标准方程;
的标准方程;
(Ⅱ)若直线 :
: 与椭圆
与椭圆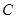 相交于
相交于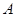 ,
, 两点(
两点( 都不是顶点),且以
都不是顶点),且以 为直径
为直径
的圆过椭圆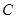 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
设函数 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值.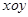 平面上点
平面上点 、
、 的坐标分别为
的坐标分别为 、
、 ,该平面上动点
,该平面上动点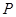 满足
满足 ,点
,点 是点
是点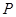 关于直线
关于直线 的对称点.
的对称点.
(Ⅰ)求点 、
、 的坐标;
的坐标;
(Ⅱ)求动点 的轨迹方程.
的轨迹方程.
如图,将边长为2,有一个锐角为60°的菱形 ,沿着较短的对角线
,沿着较短的对角线 对折,使得
对折,使得 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证:
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ)求二面角 的余弦值.
的余弦值.
已知点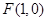 ,直线
,直线 ,动点
,动点 到点
到点 的距离等于它到直线
的距离等于它到直线 的距离.
的距离.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)是否存在过 的直线
的直线 ,使得直线
,使得直线 被曲线
被曲线 截得的弦
截得的弦 恰好被点
恰好被点 所平分?
所平分?