已知椭圆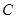 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆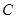 右焦点
右焦点 ,且
,且
(Ⅰ)求椭圆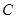 的标准方程;
的标准方程;
(Ⅱ)若直线 :
: 与椭圆
与椭圆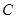 相交于
相交于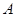 ,
, 两点(
两点( 都不是顶点),且以
都不是顶点),且以 为直径
为直径
的圆过椭圆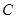 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
从1到9的九个数字中任取三个偶数四个奇数,问:
(Ⅰ)能组成多少个没有重复数字的七位数?
(Ⅱ)上述七位数中三个偶数排在一起的概率?
(Ⅲ)在(Ⅰ)中任意两偶数都不相邻的概率?
已知圆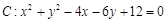 ,点
,点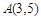 .求:
.求:
(Ⅰ)过点A的圆的切线方程;
(Ⅱ)O是坐标原点,连接OA、OC,求△AOC的面积S.
已知命题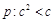 和命题
和命题 ,若
,若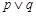 为真,
为真,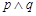 为假,求实数
为假,求实数 的取值范围.
的取值范围.
已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点 到焦点的距离等于5,求抛物线的方程和m的值.
到焦点的距离等于5,求抛物线的方程和m的值.
选修4-4参数方程与极坐标
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 ,以
,以 为极点,
为极点, 轴的非负半轴为极轴,取相同的单位长度建立极坐标,曲线C的极坐标方程为
轴的非负半轴为极轴,取相同的单位长度建立极坐标,曲线C的极坐标方程为 .
.
(1)求曲线C的直角坐标方程及直线 的普通方程;
的普通方程;
(2)将曲线C上的所有点的横坐标缩短为原来的 ,再将所得曲线向左平移1个单位,得到曲线C,求曲线C上的点到直线
,再将所得曲线向左平移1个单位,得到曲线C,求曲线C上的点到直线 的距离的最小值.
的距离的最小值.