口袋中有大小、质地均相同的7个球,3个红球,4个黑球,现在从中任取3个球。
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
某广场上有4盏装饰灯,晚上每盏灯都随机地闪烁红灯或绿灯,每盏灯出现红灯的概率都是 ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为
.记这4盏灯中出现红灯的数量为 ,当这排装饰灯闪烁一次时:
,当这排装饰灯闪烁一次时:
(1)求 时的概率;(2)求
时的概率;(2)求 的数学期望.
的数学期望.
已知矩阵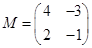
(1)求逆矩阵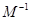 ;
;
(2)求矩阵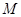 的特征值及属于每个特征值的一个特征向量.
的特征值及属于每个特征值的一个特征向量.
已知两定点 ,
,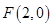 ,动点
,动点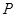 满足
满足 ,由点
,由点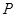 向
向 轴作垂线段
轴作垂线段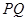 ,垂足为
,垂足为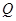 ,点
,点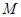 满足
满足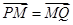 ,点
,点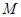 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)过点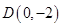 作直线
作直线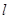 与曲线
与曲线 交于
交于 ,
, 两点,点
两点,点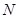 满足
满足 (
( 为原点),求四边形
为原点),求四边形 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线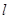 的方程.
的方程.
已知函数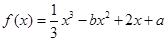 ,
, 是
是 的一个极值点.
的一个极值点.
(1)求 的单调递增区间;
的单调递增区间;
(2)若当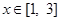 时,
时,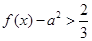 恒成立,求实数
恒成立,求实数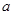 的取值范围.
的取值范围.