(本小题满分10分)某餐馆一天中要购买A,B两种蔬菜,A、B蔬菜每斤的单价分别为2元和3 元。根据需要,A蔬菜至少要买6斤,B蔬菜至少要买4斤,而且一天中购买这两种蔬菜的总费用不能超过60元。
(1)写出一天中A蔬菜购买的斤数x和B蔬菜购买的斤数y之间的不等式组;
(2)在下面给定的坐标系中画出(1)中不等式组表示的平面区域(用阴影表示),并求出它的面积。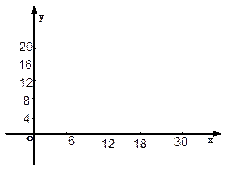
(本小题满分13分)已知函数 (其中
(其中 且
且 为常数)的图像经过点A
为常数)的图像经过点A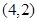 、B
、B .
. 是函数
是函数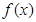 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点.
(1) 求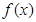 的解析式;
的解析式;
(2) 设 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列 满足
满足 ,记
,记 的前
的前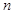 项和为
项和为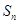 ,证明:
,证明: 。
。
(本小题满分12分)南昌市在加大城市化进程中,环境污染问题也日益突出。据环保局测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比.现已知相距18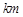 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为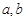 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设 (
(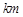 ).
).
(1) 试将 表示为
表示为 的函数;
的函数;
(2) 若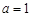 ,且
,且 时,
时, 取得最小值,试求
取得最小值,试求 的值.
的值.
(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.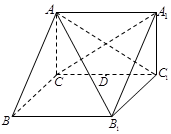
(1) 求证:平面AB1C1⊥平面AC1;
(2) 若AB1⊥A1C,求线段AC与AA1长度之比;
(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.
(本小题满分12分)已知命题p:函数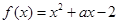 在
在 内有且仅有一个零点.命题q:
内有且仅有一个零点.命题q: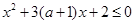 在区间
在区间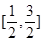 内恒成立.若命题“p且q”是假命题,求实数
内恒成立.若命题“p且q”是假命题,求实数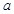 的取值范围.
的取值范围.
(本小题满分12分)设锐角△ABC的三内角A,B,C的对边分别为 A,b,c,已知向量 ,
,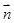
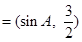 ,且
,且 ∥
∥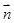 .
.
(1) 求角A的大小;
(2) 若 ,
, ,且△ABC的面积小于
,且△ABC的面积小于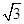 ,求角B的取值范围.
,求角B的取值范围.