(本小题满分15分)
如图,已知椭圆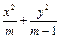 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及 直线
直线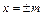 的交点从左到右的顺序为A、B、C、D,设
的交点从左到右的顺序为A、B、C、D,设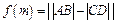 .
.
(Ⅰ)求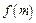 的解析式;
的解析式;
(Ⅱ)求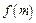 的最值.
的最值.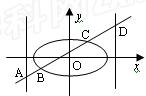
对于数列 ,定义
,定义 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .
.
(Ⅰ)若数列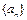 的通项公式
的通项公式 ,求
,求 的通项公式;
的通项公式;
(Ⅱ)若数列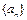 的首项是1,且
的首项是1,且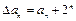 .
.
①设
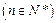 ,求数列
,求数列 的通项公式;
的通项公式;
②求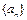 的前
的前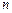 项和
项和 .
.
甲、乙、丙三人分别独立解一道题,甲做对的概率是 ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是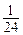 ,甲、乙、丙全部做错的概率是
,甲、乙、丙全部做错的概率是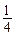 .
.
(Ⅰ)分别求乙、丙两人各自做对这道题的概率;
(Ⅱ)求甲、乙、丙中恰有一个人做对这道题的概率
在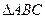 中,
中, 所对边分别为
所对边分别为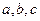 .已知
.已知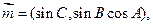
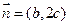 ,且
,且 .
.
(Ⅰ)求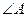 大小.
大小.
(Ⅱ)若 求
求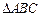 的面积
的面积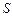 的大小.
的大小.
已知三点 、
、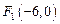 、
、 .
.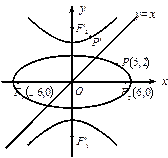
(Ⅰ)求以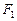 、
、 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点 、
、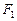 、
、 关于直线
关于直线 的对称点分别为
的对称点分别为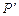 、
、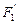 、
、 ,求以
,求以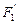 、
、 为焦点且过点
为焦点且过点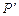 的双曲线的标准方程
的双曲线的标准方程
已知⊙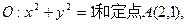 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足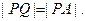
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程