(本小题12分)
已知圆C: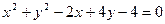 ;
;
(1)若直线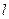 过
过 且与圆C相切,求直线
且与圆C相切,求直线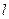 的方程.
的方程.
(2)是否存在斜率为1直线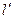 ,使直线
,使直线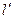 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
出直线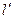 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知函数 .
.
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)当 ,且
,且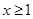 时,证明:
时,证明: .
.
二次函数 ,它的导函数的图象与直线
,它的导函数的图象与直线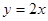 平行.
平行.
(1)求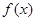 的解析式;
的解析式;
(2)若函数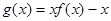 的图象与直线
的图象与直线 有三个公共点,求m的取值范围.
有三个公共点,求m的取值范围.
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比。已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). 

(1)分别写出两种产品的收益与投资的函数关系.
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
已知函数 的图像过点
的图像过点 ,且b>0,又
,且b>0,又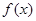 的最大值为
的最大值为 .
.
(1)将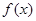 写成含
写成含 的形式;
的形式;
(2)由函数y =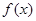 图像经过平移是否能得到一个奇函数y =
图像经过平移是否能得到一个奇函数y =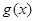 的图像?若能,请写出平移的过程;若不能,请说明理由.
的图像?若能,请写出平移的过程;若不能,请说明理由.
函数f(x)=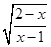 的定义域为集合
的定义域为集合 ,关于
,关于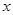 的不等式
的不等式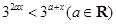 的解集为
的解集为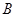 ,求使
,求使 的实数
的实数 的取值范围.
的取值范围.