(本小题12分)
已知点P(2,0)及圆C: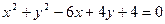 .
.
(1)若直线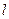 过点P且与圆心C的距离为1,求直线
过点P且与圆心C的距离为1,求直线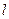 的方程.
的方程.
(2)设直线 与圆C交于A、B两点,是否存在实数
与圆C交于A、B两点,是否存在实数 ,使得过点P(2,0)的直线
,使得过点P(2,0)的直线 垂直平
垂直平
分弦AB. 若存在,求出实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知双曲线C1: (a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(1)求证:C1,C2总有两个不同的交点;
(2)问:是否存在过C2的焦点F1的弦AB,使ΔAOB的面积有最大值或最小值?若存在,求直线AB的方程与SΔAOB的最值,若不存在,说明理由。
如图,已知矩形ABCD中,AB=1,BC=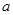
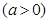 ,PA
,PA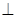 平面ABCD,且PA=1。
平面ABCD,且PA=1。
(1)问BC边上是否存在点Q,使得PQ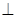 QD?并说明理由;
QD?并说明理由;
(2)若边上有且只有一个点Q,使得PQ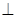 QD,求这时二面角Q
QD,求这时二面角Q 的正切。
的正切。
已知函数f(x)=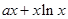 的图像在点
的图像在点 (
(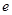 为自然常数)处的切线斜率为3.
为自然常数)处的切线斜率为3.
(Ⅰ)求实数 的值
的值
(Ⅱ)若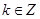 ,且
,且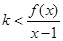 对任意的
对任意的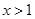 恒成立,求
恒成立,求 得最大值
得最大值
(Ⅲ)当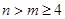 时,证明
时,证明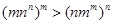
已知函数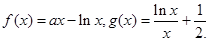
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若 ,
,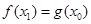 ,求
,求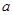 的取值范围.
的取值范围.
设函数
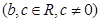 ,且
,且 为
为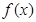 的极值点.
的极值点.
(Ⅰ) 若 为
为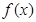 的极大值点,求
的极大值点,求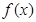 的单调区间(用
的单调区间(用 表示);
表示);
(Ⅱ)若 恰有1解,求实数
恰有1解,求实数 的取值范围.
的取值范围.