设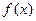 是定义在
是定义在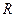 上的奇函数,当
上的奇函数,当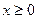 时,
时,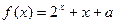 (
(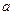 为常数),则
为常数),则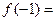 ( ).
( ).
A.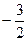 |
B.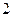 |
C.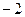 |
D.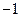 |
将函数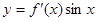 的图象向左平移
的图象向左平移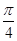 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则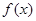 是()
是()
A.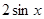 |
B.cosx | C.sinx | D.2cosx |
若抛物线y2=2px(p>0)上一点到准线和抛物线的对称轴的距离分别为10和6,则该点横坐标为
A.10或1B.9或1C.10或2D.9或2
平面内两定点A、B及动点P,设命题甲是:“|PA|+|PB|是定值”,命题乙是: “点P的轨迹是以A.B为焦点的椭圆”,那么
“点P的轨迹是以A.B为焦点的椭圆”,那么 ()
()
A.甲是乙成立的充分不必要条件 B.甲是乙成立的必要不充分条件
C.甲是乙成立的充要条件 D.甲是乙成立的非充分非必要条件
已知双曲线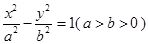 的离心率为
的离心率为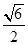 ,椭圆
,椭圆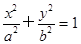 的离心率为()
的离心率为()
A.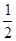 |
B.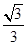 |
C. |
D. |
若曲线 的一条切线
的一条切线 与直线
与直线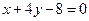 垂直,则
垂直,则 的方程为()
的方程为()
A.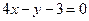 |
B. |
C.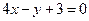 |
D. |