(本题满分13分) 在△ABC中,A,B,C分别是三边a,b,c的对角.设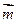 =(cos,sin),
=(cos,sin), =(cos,-sin),
=(cos,-sin),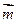 ,
, 的夹角为. (1)求C的大小;(2)已知c=,三角形的面积S = ,求a +b的值.
的夹角为. (1)求C的大小;(2)已知c=,三角形的面积S = ,求a +b的值.
已知函数 .
.
若函数 在
在 和
和 处取得极值,试求
处取得极值,试求 的值;
的值;
在(1)的条件下,当 时,
时, 恒成立,求c的取值范围.
恒成立,求c的取值范围.
已知命题p: ;命题q:函数
;命题q:函数 有意义.
有意义.
(1) 若 为真命题,求实数x的取值范围;
为真命题,求实数x的取值范围;
(2) 若 为真命题,求实数x的取值范围.
为真命题,求实数x的取值范围.
已知函数
(1)要使 在区间(0,1)上单调递增,试求a的取值范围;
在区间(0,1)上单调递增,试求a的取值范围;
(2)若 时,
时, 图象上任意一点处的切线的倾斜角为
图象上任意一点处的切线的倾斜角为 ,试求当
,试求当 时,a的取值范围.
时,a的取值范围.
已知直线l:y=kx+2(k为常数)过椭圆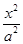 +
+ =1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
=1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
(1)若d=2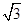 ,求k的值;
,求k的值;
(2)若d≥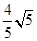 ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.
在直角坐标系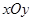 中,直线
中,直线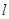 的参数方程为
的参数方程为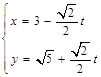 (
(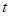 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系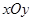 取相同的长度单位,且以原点
取相同的长度单位,且以原点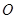 为极点,以
为极点,以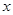 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆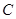 的方程为
的方程为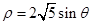 。
。
(1)求圆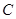 的直角坐标方程;
的直角坐标方程;
(2)设圆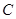 与直线
与直线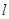 交于点
交于点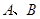 。若点
。若点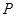 的坐标为(3,
的坐标为(3,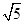 ),求
),求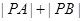 。
。