(本小题满分10分)
设函数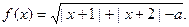
(1)当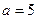 时,求函数
时,求函数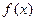 的定义域;
的定义域;
(2)若函数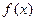 的定义域为R,试求
的定义域为R,试求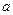 的取值范围.
的取值范围.
如图,在△ABC中;角A、B、C所对的边分别是a、b、c,且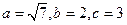 ,O为△ABC的外心。
,O为△ABC的外心。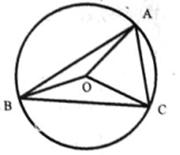
 (I)求△ABC的面积;
(I)求△ABC的面积;
(II)求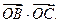
已知数列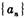 满足:
满足: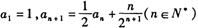
①求数列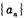 的通项公式;
的通项公式;
②证明;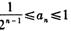
③设 ,且
,且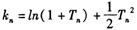 ,证明
,证明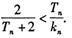
已知不垂直于x轴的动 直线l交抛物线
直线l交抛物线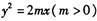 于A、B
于A、B 两点,若A,B两点满足
两点,若A,B两点满足 AQP=
AQP=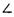 BQP,其中Q(-4,0),
BQP,其中Q(-4,0), 原点O为PQ的中点.
原点O为PQ的中点.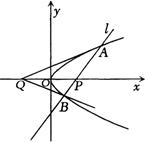
①求证A,P,B三点共线;
②当m=2时,是否存在垂直于-轴的直线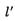 ,使
,使 得
得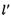 被以为直径的圆所截得的弦长为定值,如果存在,求出
被以为直径的圆所截得的弦长为定值,如果存在,求出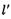 的方程,如果不存在,请说明理由
的方程,如果不存在,请说明理由
已知函数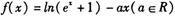 .
.
①若曲线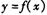 在x=0处与直线x+y= 6相切,求a,b的值;
在x=0处与直线x+y= 6相切,求a,b的值;
②设 时,
时, 在x=0处取得最大值,求实数a的取值范围.
在x=0处取得最大值,求实数a的取值范围.
在四棱锥P-ABCD中,侧面PAD丄底面ABCD,侧 棱PA="PD" =
棱PA="PD" = ,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.
,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.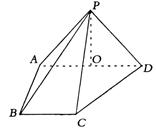
①求证PO丄平面ABCD
②求异面直线PB与CD的夹角;
③求点A到平面 PCD的距离.
PCD的距离.