（本小题满分10分）【选修4一1：几何证明选讲】
如图，已知AB是圆O的一条弦，延长AB到点C使
，过点B作
且
，连接DA与圆O交于点E，连接CE与圆O交于点F．
（1）求证：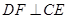
；
（2）若
，
，求BE．
（本小题满分12分）已知
，
．
（1）求
及
的值；
（2）求满足条件
的锐角
．
（本小题满分12分）若以连续掷两次骰子分别得到的点数m、n作为点P的坐标
，
求：（1）点P在直线
上的概率；
（2）点P在圆
外的概率。
（本小题满分10分）已知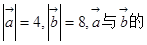
夹角是120°.
（1）求
的值，
（2）当k为何值时，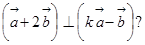
已知函数f（x）=|x+1|，g（x）=2|x|+a．
（Ⅰ）当a=0时，解不等式f（x）≥g（x）；
（Ⅱ）若存在x∈R，使得f（x）≥g（x）成立，求实数a的取值范围．
已知直线的极坐标方程为
，圆M的参数方程为
（其中θ为参数）．
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆M上的点到直线的距离的最小值．