【2015高考北京,理18】已知函数 .
.
(Ⅰ)求曲线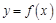 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求证:当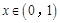 时,
时, ;
;
(Ⅲ)设实数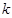 使得
使得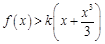 对
对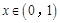 恒成立,求
恒成立,求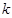 的最大值.
的最大值.
(本小题满分16分:8+8) 19
19
给出函数封闭的定义:若对于定义域D内的任一个自变量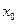 ,都有函数值
,都有函数值 ,则称函数y=f(x)
,则称函数y=f(x) 在 D上封闭。
在 D上封闭。
(1)若定义域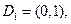 判断下列函数中哪些在
判断下列函数中哪些在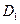 上封闭,并给出推理过程;
上封闭,并给出推理过程;
(2)若定义域 是否存在实数
是否存在实数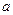 ,使函数
,使函数 在
在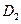 上封闭,若存在,求出
上封闭,若存在,求出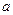 值,若不存在,请说明理由。
值,若不存在,请说明理由。
.(本 小题满分16分:4+5+7)
小题满分16分:4+5+7)
已知O为坐标原点,向 量
量
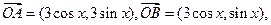
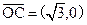 ,
,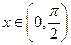
 (1)求证:
(1)求证: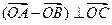 ;
;
(2) 若
若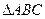 是等腰三角形,求x;
是等腰三角形,求x;
(3)求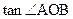 的最大值及相应的x值。
的最大值及相应的x值。
(本小题满分14分:8+6)
已知不等 式
式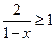 的解集为A,不等式
的解集为A,不等式 的解集为B
的解集为B
(1)求集合A及B;
(2)若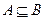 ,求实数a的取值范围。
,求实数a的取值范围。
(本小题满分14分:5+5+4)
实数m取什么数值时 ,复数
,复数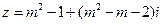
分别是:(1)实数? (2)虚数?(3)纯虚数?
(2)虚数?(3)纯虚数?
(本小题 12分)
12分)
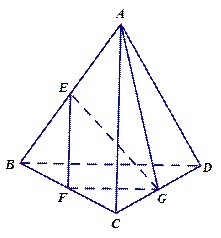
四面体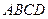 中,
中,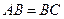 ,
,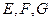 分别是
分别是 的
的 中点,且
中点,且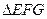 为正三角形,
为正三角形, 平面
平面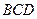 .
.
①求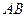 与平面
与平面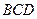
 所成角的大小;
所成角的大小;
②求二面角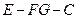 的平面角的余弦值.
的平面角的余弦值.
 |