(本小题满分16分:8+8) 19
19
给出函数封闭的定义:若对于定义域D内的任一个自变量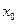 ,都有函数值
,都有函数值 ,则称函数y=f(x)
,则称函数y=f(x) 在 D上封闭。
在 D上封闭。
(1)若定义域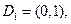 判断下列函数中哪些在
判断下列函数中哪些在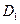 上封闭,并给出推理过程;
上封闭,并给出推理过程;
(2)若定义域 是否存在实数
是否存在实数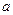 ,使函数
,使函数 在
在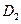 上封闭,若存在,求出
上封闭,若存在,求出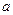 值,若不存在,请说明理由。
值,若不存在,请说明理由。
已知函数f(x)=x2+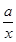 (x≠0,a∈R).
(x≠0,a∈R).
(1)判断函数f(x)的奇偶性;
(2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围.
已知二次函数f(x)满足条件f(0)=1,f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
设A,B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的只数多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为 ,服用B有效的概率为
,服用B有效的概率为 .
.
(1)求一个试验组为甲类组的概率;
(2)观察三个试验组,用X表示这三个试验组中甲类组的个数,求X的分布列和数学期望.
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的每件产品是优质品的概率都为,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品的检验费用为100元,且抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
某校校庆,各届校友纷至沓来,某班共来了n位校友(n>8且n∈N*),其中女校友6位,组委会对这n位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合”.
(1)若随机选出的2位校友代表为“最佳组合”的概率不小于 ,求n的最大值;
,求n的最大值;
(2)当n=12时,设选出的2位校友代表中女校友人数为ξ,求ξ的分布列和数学期望E(ξ).